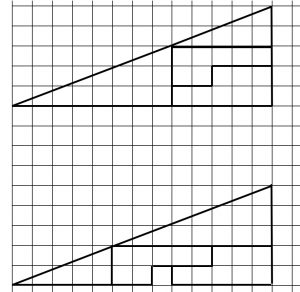
If you move the 4 pieces of this jigsaw around they will fit into both outlines. One square unit has been removed in the lower shape.
You might like to cut out the pieces from the Muggles Magic Learner Worksheet and try this for yourself.
Click here for the MUGGLES MAGIC Guide for Parents
Click here for the Notes for Teachers.
Explain what has happened to the missing area.
As Harry Potter fans know well, muggles magic is not magic at all!
See the article on NRICH Muggles, Logo and Gradients for a Logo program that throws some light on the question.
If you enjoyed this article, please consider sharing it!
5 Responses to Muggles Magic
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
Yes, so by investigating these diagrams learners can deepen their understanding of gradient provided that the teacher is wise enough to let them find out for themselves and does not tell them how the magic works .
This does not relate to Pythagoras Theorem in an obvious way but it should make you think about area and gradient
No Clinton, there is NO OVERLAPPING this is mathematics and not trickery. If you look closely at the diagrams and count the squares you can see that the 4 pieces are moved but they don’t change shape and they don’t overlap. There is more to discover here. You should consider the areas of the 4 shapes and the slopes of the top edges.
When fitted in the outline on top it looks like they form a right angled triangle with base 13 units and perpendicular height 5 units. The area therefore looks like it is 1/2 * 13 * 5 = 32.5 square units! This suggests that the parts of the jigsaw did not fit exactly in the outline of a right angled triangle as it looks-it is just visual illusion! This led to another investigation by learners whether the longest side is a straight line for it to be a hypotenuse! It appeared that the gradient is not consistent along what appears to be the longest side! The gradient of the longest side of the bigger triangle is 3/8 = 0,375 and the gradient of the longest side of the smaller triangle is 2/5 = 0.4 The ‘magic’ therefore is at the point where these longest sides of these triangles meet. The line therefore is not a straight line, it is very slightly bent in such a way that it is hardly recognisable through the naked eye because the change in gradient from 0,4 to 0.375 is so small. What looks like a right angled triangle is in fact a quadrilateral. The so called missing area has never been part of the area of the jigsaw.
Thank you for sharing with us the way your learners tackled this problem.
They started by looking at the area of the various shapes and realised that something was not quite as it should be.The areas did not add up? Why?
This led them on to checking the gradient of the hypotenuse on both triangles. They discovered they were not the same.The staight line is not straight.Therefore the shape does not have three sides but four.
The logical way that Tombi’s class tackled this problem should give other teachers some ideas on how to present this problem to their own class, which remember does not mean just showing them the solution.Think of giving them a clue if they are getting nowhere.For example, a clue could be to think about the area of the shapes.