Triangle Number Picture
 Is a picture worth a thousand words, as the saying goes?
Is a picture worth a thousand words, as the saying goes?
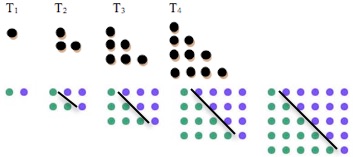
This picture shows the first 4 triangle numbers: 1, 3, 6 and 10 and how you can fit 2 identical copies of a triangle together to form a rectangle.
Can you use it to find the number of dots in the fifth triangle number without counting the dots?
Can you find any triangle number in the same way?
Can you write down a formula for the nth triangle number T_n?
Now try this! Write out this expression for the ninth triangle number:
T_ 9 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9and then write it out again underneath but this time write it backwards:
T_ 9 = 9 + 8 + 7 + … + 1.Add these two expressions together to find 2\times T_9 and a formula for T_9.
Can you use the same method to find a formula for T_n? How does this method relate to the picture method?
Click here to download the TRIANGLE NUMBER PICTURE worksheet.
Click here for Notes of Teachers.
This problem is adapted from the NRICH task Picturing Triangle Numbers with permission of the University of Cambridge. All rights reserved.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





