Wholesome Rectangles
 This activity is about rectangles with whole number dimensions. With other lengths and breadths there are infinitely many possible rectangles so here we just stick to whole numbers.
This activity is about rectangles with whole number dimensions. With other lengths and breadths there are infinitely many possible rectangles so here we just stick to whole numbers.
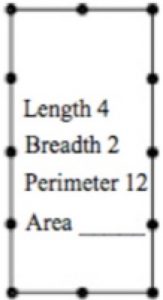
How many rectangles can you make with perimeter 12 units?
What do you know about rectangles? What is the smallest rectangle that you can make with edges that are whole numbers?
You must record your results for this activity and you could make a table to do so.
You might like to experiment by making rectangles with a chain of paper sticks or with toothpicks. See the video: How to make paper sticks.
Draw your rectangles on squared paper and record their length, breadth, perimeter and area.
Choose another perimeter and find all possible rectangles with that same perimeter. What do you notice?
Can you find other rectangles with the same perimeter and different areas?
For rectangles with the same perimeter what do you notice about the rectangle with the biggest area?
Can you find rectangles with the same area and different perimeters?
What else do you notice? Can you find connections with factors and multiples?
Click here to download the WHOLESOME RECTANGLES worksheet.
Click here for the Notes for Teachers.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





