Powerful Thinking 4
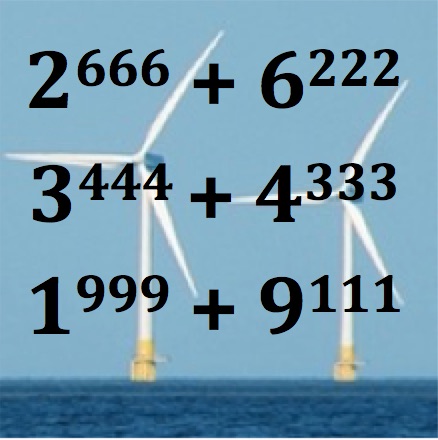 Is this number 3^{444} + 4^{333} divisible by 5?
Is this number 3^{444} + 4^{333} divisible by 5?
Hint: Just look at the last digits of powers. What values do they take?
Investigate other big powers?
Make up some similar numerical expressions involving powers that have interesting properties.
What about even bigger powers 2^{666} + 6^{222} or
7^{888} + 8^{777}?
Click here for the POWERFUL THINKING 4 Worksheet.
Click here for Notes for Teachers.
Click here for the poster.
This problem is adapted from the NRICH task Big Powers with permission of the University of Cambridge. All rights reserved.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





