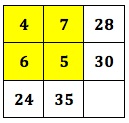
In the first square the boxes at the end of each row and the foot of each column give the result of multiplying the two numbers in that row or column.
Can you find 4 consecutive numbers to complete the second multiplication square in the same way?
Make up puzzles for your friends like this one.
MAKE UP YOUR OWN PUZZLES Put 4 consecutive numbers into a 2 by 2 square, work out the products. Then give your friends the products (not the 4 consecutive numbers). Can they find 4 consecutive numbers and put them in the right places to get your products?
The 3 by 3 multiplication square works in the same way. The boxes at the end of each row and the foot of each column give the result of multiplying the three numbers in that row or column. Can you use the digits 1 to 9, each once and only once, to give the correct products of the 3 numbers for each row and column?
MAKE UP YOUR OWN PUZZLES For the 3 by 3 multiplication puzzle, put the numbers 1 to 9 into a 3 by 3 square in any order, then work out the products, then give your partner just the products and challenge them to put the digits 1 to 9 in the right places.
See Notes for Teachers – Multiplication Squares and more about the problem on the NRICH website http://nrich.maths.org/757
If you enjoyed this article, please consider sharing it!
5 Responses to Multiplication Squares
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
My learners do the problem of two by two numbers it was easy to them.The three by three numbers is a little bit difficult.I gave them a skill of finding the first three numbers,then take number in the last row and divide it by the number in its column then look at the answer and check the numbers that can multiply that number and verify the by multiplying all three numbers wether they give up the product at the last column or row.
Nikie, from what you describe your learners had some good practice in multiplying and finding factors.
What grade do you refer to?
CAPS for Grade 6 (see page 10) says you must teach: Multiples of 2-digit and 3-digit numbers; Factors of 2-digit and 3-digit numbers; Prime factors of numbers to at least 100.
If you are teaching grade 6 you could teach them how to find prime factors. Then your learners could make up their own puzzles exactly like the one given, as suggested, and other learners could solve them using the prime factors.
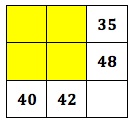
Msuthu, this activity needs knowledge of x-tables, and is also good for practicing tables, multiples,etc. If we look at the one where the square looks like this:
… … 35
… … 48
40 42 …
we now need to fill the empty spaces. Your learners need to find four consecutive numbers in such a way that the product in the top horizontal row equals 35 and the product in the first vertical column equals 40. Then the same for the 2nd row and 2nd column. NB! The four numbers to fill these 4 spaces must be consecutive, for example: 5, 6, 7, 8 or 1, 2, 3, 4 or any other four consecutive nrs. that work.
Hope this helps.
I did the magic square with my learners 3 weeks ago. I discuvered that for them it was easy to deal with simple problems but as I used larger products then they got completely confused. I think that even though they processed the simpler numbers, I did not give them enough chance to explain how they did it. The bigger the number, the diffucult it became to work with mental. I had done lots of multiple work with them but it challenged them. Mce
i did multiplication squares with the grade 4 learners. since it is grade 4 learners i started from simple 2 by 2 table my learners did a a puzzle with 2 by 2 numbers. i gave them instructions, i used numbers like 20, 30, 40 for their understanding. they knew their factors , i told them about prime numbers the meaning.