Currently viewing the tag: "Length"
Let’s walk from here to that tree,
How many paces will that be?
Spread your fingers as wide as you can,
What you have now is called a hand span .
A hand span can help you to find out how big
Is the height of a cow, a […]
An aluminium can contains 330 ml of cola.
If the can’s diameter is 6 cm what is the can’s height?
Suppose the can’s height is 10 cm, what does the diameter have to be?
Which of these two cans uses the least aluminium?
If you could choose any diameter which dimensions for the can […]
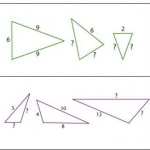
Each picture shows 3 similar triangles.
They are called similar because they are the same shape, they have the same angles and the lengths of the edges are in the same ratio. For example in this diagram the edges in each triangle are all in the ratio 2 : 3 : 4 […]
Draw chords to cut a regular hexagon
(a) into two pieces which, when put together, make a parallelogram;
(b) into three pieces which, when put together, make a rhombus;
(c) into four pieces which, when put together, make two equilateral triangles.
(d) What angles can you find in each of your shapes?
(e) If […]
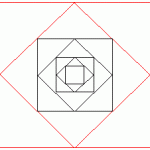
Seven squares are drawn inside each other. The centre points of each side of the outer square are joined to make a smaller square inside it and so on.
The centre square has the area of 1 (one) square unit.
Draw the diagram. You can download square dotty paper here.
What is […]
Show that is it impossible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units.
Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units?
Can you write general rules for someone else to use to check whether […]
Bilbo decides to leave his hobbit-hole and go on an adventure. He walks 100 km South, then 100 km East, then finally 100 km North, at which point he is surprised to find that he has arrived back home!
Many people would think that because of this Bilbo must live at the North Pole. […]
Little Man is much smaller than you and me. Here is a picture of him standing next to an ordinary mug.
Can you estimate how tall he is? How tall do you think Little Man’s mug might be?
My mug is 10 centimetres tall and it holds 300 millilitres but mugs come in different […]
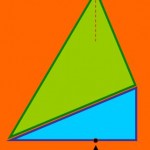
Two right-angled triangles are joined as shown in the diagram.
The green triangle has side lengths of 65, 52 and 39 cm and the blue triangle has side lengths of 52, 48 and 20 cm.
An object is dropped vertically from the top of the green triangle hitting the base by […]
FOLLOW US ON SOCIAL MEDIA
