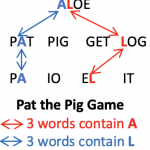
PAT THE PIG is a game for two players or two teams. Take it in turns to choose one of the words. Aim to collect 3 words that contain the same letter and to stop your opponent from doing so. The winner is the first to get all 3 occurrences of the same letter. Continue […]
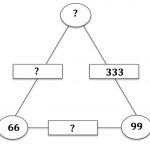
The FIFTEEN GAME is a game for two players (or a class split into two teams).
Take it in turns to choose one of the numbers 1 to 9. It is now your number and your opponent cannot choose it. Each number can be chosen only once.
To win, be the first to pick 3 […]
? + ? = 2025. How many ways can you replace the ? marks with whole numbers, or put whole numbers in the boxes, to make the sum correct?
Here is one way to do it. How many other ways can you find? Explain your answer.
Now […]
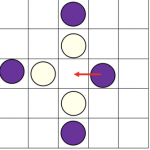
Start with the easiest version on a 25 square board each player having 12 men (coloured counters). Then graduate to boards with 49 or 81 squares and 24 or 40 men each. Either 25 or 49 squares can be used on the board shown. Aim to set traps to capture your opponent’s pieces and to […]
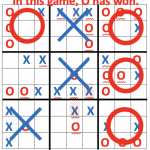
Two players (X and O) play 9 simultaneous games of Tic Tac Toe on a 9 by 9 mega-board taking turns to put their mark on one of the 81 squares. X starts. The position chosen by a player on the 3 by 3 mini-board forces the next player to play on […]
Put 11 cards numbered 2 to 12 into a bag. Each player then draws a card giving them a horse. If there are fewer than 11 players, they can draw more than one horse. To assign the last few horses, players throw a die and, if they throw a six, they draw another […]
SQUARE GAME. Download the net and make a tetrahedral dice.
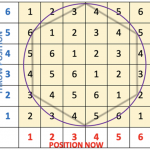
All players have 4 counters and put one anywhere on the top row of the gameboard. Players throw the dice in turn, using the Square Game key-table to find out where to go next, […]
At the start, the game pieces (or counters) are arranged as shown. In turn, the players throw the 4 sticks to determine the number of houses to move, the piece on house 10 moves first, they move through the squares, (called houses) in the order shown by the numbers and, if they […]
There are 36 cards with a picture on one side and a description on the back. Shuffle the cards. The first player takes the top card and, taking care to avoid showing either side of the card to the other players, describes the image giving clear instructions for the other players to […]
The Checkit Game is suitable for all ages because you can choose the type of numbers and the operation that you will use.
You can play this game with different sets of numbers like whole numbers or integers, fractions or decimals and with (1) addition and subtraction or with (2) multiplication and […]
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC