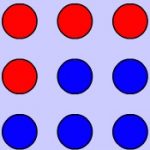
(a) You must mark four red squares and five blue squares in a 3 by 3 grid .
How many ways can you do this so that all the rows columns and diagonals have an even number of red squares?
Two solutions are considered the same if one can be transformed to […]
Suppose you had the never ending task of writing out all the natural numbers: 1, 2, 3, 4, 5…. and so on.
What would be the 1000th digit you would write down?
In what number would it occur?
What number would contain the millionth digit?
When would you have written six for […]
Think of a whole number. Square it. Subtract the number you first thought of. Is the answer odd or even?
Try this with other numbers. What do you notice? Can you explain why? Can you find different ways to explain (and prove) the result that you noticed. You might use what you […]
My car has number plate – S208VBJ.
Using my special code S208VBJ adds to 65.
Using the code every character, a digit or a letter, is separate.
Numbers are simply added together so that, in the first number plate 208 is 2 + 0 + 8 = 10.
Letters are translated into […]
If you change the order of these digits you can get 24 different numbers, for example 2547, 2574, 2745, … Can you find all 24 different numbers made by using each of the digits 2, 4, 5, 7 just once?
How many of these numbers have 2 in the thousands place? How many have 2 […]
Using the numbers 1, 2, 3, 4 and 5 once and only once and the symbols × and ÷ once and only once, what is the smallest whole number you can make?
Now suppose you have to use the symbol + once and the symbol ÷ twice what is the smallest fraction […]
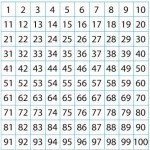
A hundred square has been printed on both sides of a piece of paper.
One square is directly behind the other.
What is on the back of 100? 58? 23? 19?
Can you see a pattern?
Click here for the HUNDRED SQUARE Notes for Teachers.
Click here for the HUNDRED […]
What do the digits in the number 15 add up to?
How many other numbers up to a thousand have digits with the same total if we only include numbers without zeros?
Click here for Solutions and Suggested Lesson Plans in the AIMSSEC Notes for Teachers.
This problem is adapted from the NRICH […]
Little Man is much smaller than you and me. Here is a picture of him standing next to an ordinary mug.
Can you estimate how tall he is? How tall do you think Little Man’s mug might be?
My mug is 10 centimetres tall and it holds 300 millilitres but mugs come in different […]
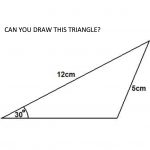
Imagine you have a pencil, ruler, protractor and compass and you try to draw this triangle. Is it possible?
If you have geometry instruments then try it for yourself. What do you notice?
Can you give reasons for your answer to the question “Is it possible?”
Click here for The Notes for Teachers. […]
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC