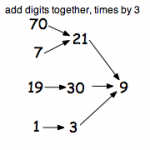
Follow some numbers and see where they go.
The simple rule is: choose a number, add the digits together then multiply by 2 and then do the same again.
Suppose you start with 56 then you get 5+6 = 11 and 11 x 2 =22 so the next number is 22. Carry on and you […]
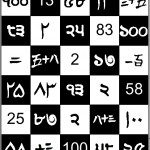
There are six numbers written in five different scripts.
Can you sort out which is which?
Write 51 in each script.
Click here for Notes for Teachers.
This activity was initially developed by SMILE (Secondary Mathematics Individualised Learning Experiment) by practising teachers in London in the 1970’s as one of a series of […]
Write down three consecutive whole numbers none of which is a multiple of three. If you can’t do it, explain why.
Multiply any two consecutive even numbers together. Why is the product always a multiple of eight?
Take any prime number greater than 3, square it, subtract one and divide by 24.
Make a […]
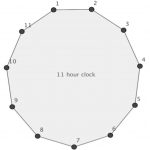
In his grid, how many pairs of numbers can you find that add up to a multiple of 11?
Do you notice anything interesting?
Can you see a connection with the 11-hour clock?
Can you find all the pairs?
Could you convince someone that you haven’t […]
Show that is it impossible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units.
Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units?
Can you write general rules for someone else to use to check whether […]
Various pairs of numbers add together to give a sum of 10:
3 + 7 = 10
2 + 8 = 10
4.4 + 5.6 = 10
The products of these numbers are all different:
3 x 7 = 21
2 x 8 = 16
4.4 x 5.6 = 24.64
[…]
You can weigh all integer masses from 1 to 60 with 6 weights putting the weights in one pan and the object in the other pan. Which weights are used?
What about weighing all integer masses from 1 to 1000?
What about from 1 to n?
What could this have to do with the […]
Bilbo decides to leave his hobbit-hole and go on an adventure. He walks 100 km South, then 100 km East, then finally 100 km North, at which point he is surprised to find that he has arrived back home!
Many people would think that because of this Bilbo must live at the North Pole. […]
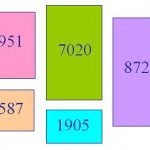
What is the largest number that, when divided into each of 1905, 2587, 3951, 7020 and 8725, leaves the same remainder each time?
When a problem seems difficult a good strategy is to try a simple case.
The diagram should help you to find the answer to the same question […]
(a) You must mark four red squares and five blue squares in a 3 by 3 grid .
How many ways can you do this so that all the rows columns and diagonals have an even number of red squares?
Two solutions are considered the same if one can be transformed to […]
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC