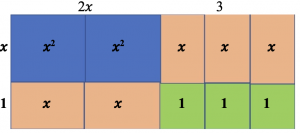In this game players solve jigsaw puzzles and find the factors of quadratic expressions by fitting pieces together to make rectangles. To factorize the expression $ax^2 + bx +c$, where $a, b$ and c are positive, players must arrange into a rectangle: a blue $x^2$ pieces, b brown $x$ pieces and c green unit pieces. The diagram shows $2x^2+5x + 3=(2x+3)(x+1)$.
Rules: Each pair (or group) of players needs an envelope with at least 20 blue x2 pieces, 20 brown x pieces and 30 green unit pieces. The teacher needs to have a list of quadratic expressions that can be factorized and a few that cannot.
- The teacher writes a quadratic expression on the blackboard. The first pair or group to make a rectangle with the pieces and find the factors wins the round.
- The winning pair should explain to the class how they solved the puzzle, and all the learners should copy the solution diagram into their notebooks.
- This can be repeated for other quadratic expressions.
Extra challenge: The game can include a few quadratic expressions that cannot be factorized. In this case the winners are the players who can prove that the expression cannot be factorized and explain why.
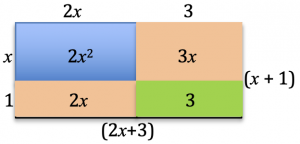It helps to visualise the finished rectangle as four smaller rectangles with the blue pieces in the top left, the green pieces in the bottom right, and the brown pieces at the top right and bottom left. Learners can make simplified sketches as in this example, which don’t need to be drawn to scale.
Click here to download the Notes for Teachers.
Click here to download the Algebrarea Game Worksheet and Puzzle Pieces
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
